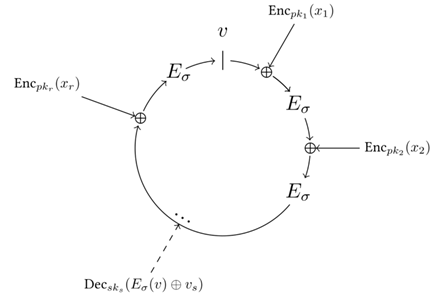
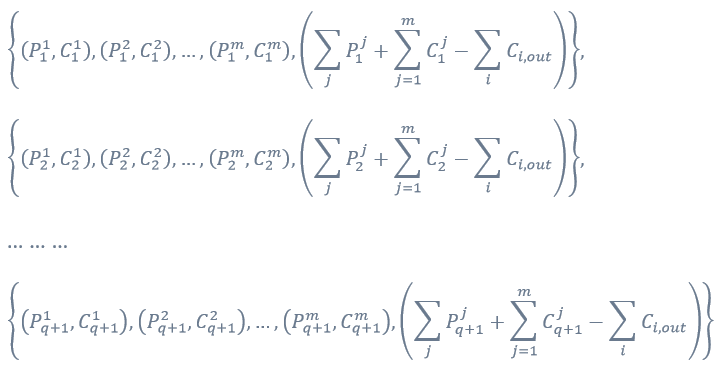The QURAS Blockchain implemented the anonymization of the transaction by realizing the encryption of the transaction contents.

The basic problem of anonymizing transactions is how to verify the contents of the encrypted transaction from the Consensus Node.

That is, the Consensus Node must be able to prove that the encrypted transactions are accurate without the use of decryption keys for encrypted transactions.

In order to implement this, the Zero-Knowledge Proof, a zero-knowledge encryption algorithm, can be used to verify the accuracy of encrypted transactions even without a real decryption key (private key) on the Consensus Node.

The ZK - SNARKS is a module that implements this ZKP.

Let's start by looking at the concept of Zero-Knowledge Proof.

The zero-knowledge proof method is a cryptographic theory, which proves what kind of equation is true to the opponent without exposing any information.

A prover is the one which tries to prove that any kind of equation is true, and the one which participates in a certification process and exchanges information with a prover is called a verifier.

When a prover participates in a zero-knowledge certificate and modifies a protocol with the purpose of cheating the verifier, the prover is untruthful, otherwise truthful.

The zero-knowledge proofs must satisfy such as the following 3 properties:

1. Completeness: If any kind of equation is true, a truthful prover must be able to prove that the equation is true to a truthful verifier.
2. Soundness: If any kind of equation is false, any untruthful prover must convince an untruthful verifier that the equation is true.
3. Zero-Knowledge: If any kind of equation is true, the verifier must know nothing except for the authenticity of the equation.

The zero-knowledge proofs depend on the probability theory.

A typical example is the Ali Baba cave problem.

That is to say if the number of proof execution increases between the prover and the verifier, the accuracy of the proof of the equation becomes higher.

However, it is inconvenient to use the proof of execution between the prover and the verifier in the QURAS Blockchain.

The proof method based on the probability theory becomes the Interactive Zero Knowledge Proof.

That is to say, it is an algorithm which judges true and false of the equation as the probability of true and false by carrying out the execution many times.

Such a system causes various problems such as a load on the network.

Then, the concept of non-interactive zero-knowledge came out. [7] [8]

The verification for proof, however, is due to the estimation of the calculation.

Non-interactive zero-knowledge proof is a method to perform verification without interacting with the prover as a type of ZKF.

ZK-SNARK (Zero-Knowledge Succinct Non-interactive Argument of Knowledge) is a concept brought up by non-interactive zero-knowledge proof, and it is also used in the Z cash.

Since there are many publications related to zero-knowledge, please refer to the reference to the specific contents.

ZK-SNARK (Zero-Knowledge Succint Non-interactive Argument of Knowledge) does not exchange any information between the prover and the verifier, however, the prover creates a proof scheme and provides a module that can be varified by the verifier. As an example, in the provider of that proof scheme, there is an algorithm that can be used to inform that it has the Secret Key.

At this time, the verifier will not be able to find any information, such as the prover’s Secret key in the proof scheme.

The ZKP (Zero-Knowledge Proof) is a method in which the prover verifies that a proof scheme is correct without giving any related information.

As an example, if the Hash Value B for random number A can be used, at some point, to verify to the verifier that the prover knows that A corresponds to the Hash Value B, without showing A Value.

The Proof of Knowledge in zero-knowledge is a method which makes it clear that not only has A in the verifier, but it also that the value is accurate without showing A.

In Succinct ZKP, the verifier can determine whether the prover's proof is true or false, regardless of its length, in a short period of time (some ms second).

The Interactive ZKP was able to end up with proof originally after a couple of times the prover and the verifier had been able to communicate.

Therefore, the verifier sent a variety of commands to the prover for verification, and it was possible to determine true and false probability of a certificate based on the probability theory.

In this case, the prover is designed so that the prover's secret data can not be found as a command sent by the prover or a command sent by the verifier.

However, the Non-interactive ZKP allows only one command between the prover and the verifier to be used to determine the true and false authenticity of a verification scheme.

In order to implement the Non-interactive ZKP, the Public Parameter aiming at zero-knowledge algorithm between the prover and the verifier needs to be shared.

The QURAS Development Team will proceed for the key, and it will commonly be used in the QURAS Blockchains.

Before looking at DAP(Decentralized Anonymous Payment System)used in the QURAS blockchain, it is necessary to first examine the centralized payment system that is used by banks.

Anonymous E-Cash : This was developed by Chaum. Chaum’s logic is as follows:

1. Let’s assume that Alice and a bank have coins. In order to create coins,the value of which is equivalent to v, Alice first selects a random secret number, or SN, that the bank would not know. Then, the portion of v is withdrawn from Alice’s account, and the bank signs the SN. Next, when Alice tries to send Bob some of her coins, she grants the bank-signed SN to Bob to prove that the signature was truly by the bank. When doing so, neither Bob nor the bank would have access to Alice’s personal identifiable information from the SN information. Also, the bank monitors the SN for past occurrances in order to prevent double payment.

Unforgeable E-Cash : There is one problem in the Chaum’s logic; the possibility of coins being counterfeited when a bank’s secret key is compromised. The following example illustrates this flaw in more details:

1. A bank maintains Merkle Tree as “Coin Commitment”, and a user regularly references “rt” which is the root value of this Merkle Tree. The bank does not maintain any secret documents. When Alice requests coins, she selects a random secret number (SN) and the auxillary string r to calculate cm:=CRH(SN||r) and send it to the bank. Here, CRH is a collision-avoidance function.
2. Once the bank receives cm, it reduces the requested amount from Alice’s account and add cm to leaf nodes to Merkele Tree. After that, to pay Bob, Alice sends zero-knowledge proof π along with SN.
3. Alice may inform Bob that SN is stored in Merkle Tree’s leaf. However, due to the zero-knowledge proof, Bob does not know Alice’s personal identifiable information. Later on, Bob sends the bank the SN and πhe received from Alice.

First, before knowing the principle of zk-SNARKs, let’s look at the Transparent Transaction in QURAS Blockchain, and see whether we can use the zk-SNARKs for an item to implement the anonymous.

A typical Transparent Transaction is viewed from a Contract Transaction structure.

The basic input in the Contract Transaction is the Coin Reference information, and it is an item of output and the Transaction Output.

From, To, and Amount information for the Transparent Transactions in a QURAS Blockchain is derived from the items in the Contract Transaction's Coin Reference and the Transaction Output.

Let's look at how From, To, and Amount can be determined from the items in Contract Transaction's Coin Reference and Transaction Output.

In the Contract Transaction structure, Coin Reference is a reference to the Transaction output of the previous Transaction.

In other words, you can deduce Coin Reference from blockchain data to easily obtain the item of the Transaction Output that Coin Reference represents.

The item in the Transaction Output has 3 items: AssetID, Value, and Script Hash.

That is, the Script Hash of the item in the Transaction Output pointed to by the Coin Reference is From's address.

Then, the Script Hash of the Transaction Output item in the Contract transaction will show the final balance status.

That is, the address of To and the amount of remittance can be confirmed by this item.

All the items in the Contract Transaction are not encrypted, but they are registered in the blockchain as they are, so that the node can accurately check whether the resulting transaction could accurately calculate From, To, and Amount, and check the sign value to see if the transaction was forged or not.

Now, you'll find out about the part of the Anonymous Transaction that needs base encryption.

The parts that must be encrypted in the Anonymous Transaction are the Coin Reference and items in the Transaction Output.

Using a zero-knowledge proof algorithm for this part will not allow a node to speculate on From, To, or Amount of money, so that the anonymization of the transaction can be implemented.

So, let’s move on to how the Coin Reference and the Transaction Output in encrypted, and then how it try to figure out what other nodes can verify that it is accurate.

In QURAS blockchain, an address and transaction for zk-SNARKs are different from a transparent address.

In QURAS blockchain, the address generation portion for zk-SNARKs is omitted, as explained in an earlier part of this document.

As described in the QURAS blockchain section, the reference and the output portions are fully encrypted. A verifier needs to verify the encrypted content without a private key.

That is when ZK-SNRKS, which is a new concept, comes into play.

The concept includes commitment and nullifier.

Let’s display a balance that is encrypted in QURAS blockchain as “Note”. When that happens, the concept of Note can be seen as UTXO for Bitcoin.

However, Note is encrypted while UTXO is transparent.

The following exemplifies how verifier verifies Note:

During an anonymous transaction, there are two concepts: commitment and nullfier.

Commitment can be considered an upspent note. In Bitcoin, it is the same as an upspent UTXO.

Nullifier is created to prevent a double payment, but this is also a spent note.

A reference entry in a transaction uses nullifier to make hash public in blockchain.

For a transaction output, commitment is made public at each hash value.

Hash function is a one-way function that means it is possible to find the Y value from x->Y by x, but going the opposite way is difficult.

For zk-SNARKs, hash function is used often.

First, a hash function is used in commitment markle tree.

Markel tree is structured by creating a binary tree by setting JointSplit’s commitment value as leaf. When doing so, the hash function is used.

Also, when calculating hSig for JointSplit, the hash function is used.

The PRF function indicates a random function.

In QURAS blockchain, PRF is re-built based on C# random function.

Many PRFs are used to generate JoinSplit.

PRF started being used because of the unpredictability of encrypted Cenc and for preventing the repetition of commitment.

The characteristics of PRF function are such that, when an x value changes, the result of PRF (x) must always change.

Authenticated One Time Symmetric Encryption can be expressed simply using SYM.

When SYM.K(SYM key)is used to encrypt the plaintext SYM.P to SYM C, SYM is defined as follows:

1. SYM.Encrypt : a function to convert SYM.K × SYM.P=> SYM.C
2. SYM.Decrypt : a function to convert SYM.K × SYM.C=> SYM.P
3. It is recommended that this type of SYM function is used only once.
1. This function may be attacked by an attacker once its SYM. K is made public, so it is strongly recommended that it is used only once.

A key agreement format is a cryptgraphic protocol in which two people (for example A and B) use their own public key to promise shared secret documents.

In other words, A’s and B’s key can be used to share secret documents that can be seen only by A and B.

This means, third parties do not know the secret documents A and B shared.

A key agreement format (hereafter KA) is embodied as the following 3 elements:

• KA.Public : Public Key used by B
• KA.Private: Private Key used by A
• KA.SharedSecret: Secret document that cannot be seen by any other people than A and B.

KA can be examined by defining the following functions:

1. KA.FormatPrivate: This function is used to create a random byte string using KA. Private.
2. KA.DerivePublic: This function is used to generate a KA.Public using KA.Private and KA.base.
3. KA.Agree: This function is used to create a KA.SharedSecret using KA.Private and KA.Public.
4. KA.Base: This is a basic value of KA.Public.

A key agreement protocol was created to resolve the problem with Diffie-Hellman’s key exchange.

The downside of Diffie-Hellman’s key exchange protocol is that no authentication against A and B can be done when exchanging a key between A and B.

In other words, it is possible to exchange anyomous keys between A and B by using a key exchange protocol, but it is vulnertable when a third-party (C) is trying to intercept between A and B.

During a key exchange between A and B, C could enter between the two and exchange a key with A and B individually. Once such exchange is complete, C can intercept data exchanged between A and B.

As a countermeasure, a method was adopted that sends a signature by using a key that is generated by a third-party authentication institution. In other word, this is a method to prevent the third-party C from intercepting between the two.

Key Derivation function is a function that is defined by combining key agreement and authenticated one-time symmetric encryption.

This function generates a key that is used for shared secret data which is generated by combining a key agreement and multiple arguments for encryption.

KDF(Key Derivation Function) is defined as follows:

{1… N} × Bytes(hSig) × KA.SharedSecret × KA.Public × KA.Public => Sym.K

The above function is the KDF function.

The following security conditions are needed to satisfy KDF:

ESK and EPK are generated according to the above method.

By using KDF to generate a secret key between a coin sender and his recipient and reflecting the information on the transaction, only a receipent can decode the encryption.

A Sig can be defined as follows:

A sender uses the above Sig function to create and sign a transaction and have it transferred.

Zero-knowledge authentication system is an encryption protocol that proves one’s legitimacy without having to expose any information to a verifier.

Zero-knowledge authentication system is used for verification by encrypting a transaction at the QURAS block change according to zk-SNARKS.

In Quras blockchain, the following key is generated beforehand so that zk-SNARKS can be used:

In other words, a verifier uses zk.ProvingKey, zk.PrimaryInput and zk.AuxiliaryInput to generate zk.Proof, and has it transferred by entering the zk.Proof data and the zk.PrimaryKey into the transaction.

The person who performs verification upon receipt of a transaction may use; ZK.VerifyingKey and ZK.PrimaryInput/ZK.Proof in the transaction, to process verification based on its True or False authentication result.

There are four elements in the zk-SNARKs KEY:

a_sk, a_pk, sk_enc, pk_enc

Here, a_sk is a 32-byte random byte array as a sending key.

The three remaining keys of a_pk, sk_enc, pk_enc are all generated from a_sk.

The generation principle is as follows:

a_pk= PRF_addr(a_sk,0)

sk_enc=KA.PrivateKey(PRF_{addr(ask, 1})

pk_enc=KA.PublicKey(sk_enc, KA.Base)

Here, the PRF function and the KA function are not mentioned as they were explained earlier in this document.

There is more than one JoinSplit item for an encrypted transaction.The JoinSplit items included in anencrypted transaction are JoinSplitSig and JoinSplitPubKey.

A verifier verifies the authenticity of JoinSplit through JoinSplitSig, JoinSplitPubKey, and JoinSplit.

Also, zk-SNARKs Verify Key from an item in JoinSplit is utilized to verify the correctness of the JoinSplit content, which, in other words, is zero-knowledge authentication.

The following are items that exist in JoinSplit:

• VAmount_Old : When transferring money to T(transparent account)->A(anonymous account), this diplays the balance in transparent.
• VAmount_New : This displays a balance that goes into T account if T->A or A->T.
• MerkleRoot : This is Markle Tree’s root hash value for commitment until the previous block.
• Nullifier(1, 2) : This means a Nullfier for two nodes that went into Input.
• Commitment(1, 2) : This means a commitment value for a note that is recorded in Output.
• Epk : This is a public key in KA key pair that is used to encrypt output note. When that happens, output is encrypted by connecting the ESK and a recepient’s PKenc. In other words, the recipient can decode the encrypted Cent that were encrypted by using his own SKenc and EPK. 
• RandomSeed : This means a random byte sequence for calculating the proof value of JoinSplit. 
• Proof : This indicates ZE-SNARKS’zero-knowledge authentication data for JoinSplit.
• Cenc : This indicates the encrypted data of note.

No values of VAmount_Old and VAmount_New can be more than 1.

In the case that all of those values are greater than 1, the transaction is considered a failure.

If zk-SNARKs authentication is true when it is done through JoinSplit’s proof and ZK-SNARK Verify Key, the transaction is considered a success.

If it is not true, the transaction is considered a failure.

The encrypted transaction is composed of more than one JoinSplit item.

When JoinSplit is composed, during the first phase, a key pair for a signature key (JoinSplitSig) needs to be generated first to verify JoinSplit.

A key pair, JoinSplitPrivKey and JoinSplitPubKey, is generated as a key generation based on ECC algorhythm.

After that, items for JoinSplit are built.

JoinSplit items are composed of two Inputs and two Outputs.

A sender composes Input items as follows:

• If there is one note that is applicable to Input -> A random note is generated to create two Inputs.
• If there are two notes that are applicable to Input -> two will be created in Input.

While generating Input, hsig is generated. Then, a random byte sequence is generated and based on such sequence, Output is generated.

The following is the phase to generate Output:

• Select one random byte sequence. The length is a 32-byte sequence.
• Let’s assume that I is an index for Output. {0, 1}
• Calculate as ρi=PRF(i, hsig)
• Lastly, encrypt note for a recipient’s pk_{enc, i}

Here, the purpose of inserting a random letter sequence in Input and Output is to make encryption decoding difficult.

In other words, even if the balance and the address for the note are the same, the generated encrypted data in the generated note is different depending on random sequences.

Like the above, random letter sequences are inserted for not informing that the users have the same notes.

When JoinSplit generation is complete, after JoinSplit body part is signed with JoinSplitPrivKey, JoinSplitSig is inserted in the transaction so that the transaction generation is complete and broadcasted to blockchain. 

Let’s assume that the depth of Note Commitment tree is MerkleDepth.

Each node for Merkle tree is composed of hash value.

Merkle tree, of which height is h, has the maximum node of Pow(2,h) unit and the minimum node of Pow(2,h-1) unit.

In Merkle tree, the note at the last level is called “leaf note”.

In Merkle tree, nodes that exclude leaf nodes and route nodes are called internal nodes.

Let’s assume that M(h,i) is the “ith”node in Layer h.

Here, the computation formula of M(h,i) is as follows:

M(h, i) = MerkleHash(M(h+1, 2*I), M(h+1, 2*I + 1))

In Quras blockchain, based on Auth Path theory, the route value and the correctness of Merkle Tree can be verified.

In anonymous transaction, it was described that there are JoinSplit items.

In JoinSplit items, VAmount_old means pulling coins out of Transparent balance pool while VAmount_new means putting coins in Transparent balance pool.

Users can simply measure the balance of the QURAS blockchain’s overall transparent balance pool through JoinSplit and VAmount_old.

Other applicable accounts cannot be viewed.

In JoinSplit, account management is done per encrypted note. 

Every note is stored while it remains encrypted in blockchain. This encryption can be referenced only by users who have the key to the account.

Anonymous Transaction has more than one JoinSplit item, but when a transaction enters a blockchain, JoinSplit’s commitment is added to the blockchain’s note commitment Merkle Tree.

Also, JoinSplit’s Nullifier will be registered with the blockchain.

When an anonymous transaction is registered with a blockchain, if Tx Nullifier is already registered with the blockchain, it is recognized as a double spend and brought back to failure without registering the transaction with the blockchain. 

When a random string is inserted into the note, Nullifier values are different for the same note, so double-spend can be prevented as nullifier.

Ring signature is one of the electronic signature algorhythems that is executed by the signatures of all users who have a key and participates in the group.

The ring signature method allows any users of a group which has a key to sign, meaning that a document that is signed using a ring signature is waranteed by a user of the specific group.

The characteristic of ring signature is that what kind of user key is used within a group is unknown. While ring signature is often compared with group signature since they are extremely similar, they are diffent in the following characteristics:

• Anynomity cannot be disposed
• There is no group’s administrator
• No additional actions are necessary for any group users to be a user of other groups.

In other words, a message with ring signature is approved by a certain user in a group. The basic characteristic of a ring signature is that it is hard to decide which user in a group signed the ring signature.

A ring signature is similar to a group signature, but there are two differences:

• The anonymity of an individual signature cannot be known.
• Voluntary users in a group can participate to form a group without additional settings.

Definitions of a ring signatures are as follows:

All of the users in a group have to have a pair of public key and private key.

That said, N units of user group can be defined by (P1, S1), (P2, S2), ···, (Pn, Sn)

Assuming, for example, that a ring signature from “I”th user against Message m is σ,at that point all users can verify a ring signature based on the ring signature σ, m,  P1, P2, …, Pn.

 

If the ring signature is calculated, it will pass at the verification.

Unless users’ private keys are within a group, it is difficult to calculate a correct ring signature.

The structure of ring signature consists of 2 processes – Ring-sign and Ring-verify.

• Ring-sign(m, PK1, PK2, …, PKn, i, SKi) : A process to generate a signature value σ for a document m by using a group users’public key for n number of people and Ski, a secret key for the“i”th number of group user.
• Ring-verify(m, σ) : A process that verifies a signature by using a signature σ that includes a public key by a document m and all group users.

Ring signature does not require group members to be added or deleted because a signer may sign as long as group users’ public key is known. However,a signature value needs to include user keys of users in a group, so the downside is that a signature value needs to be longer as the number of members increase.

This application is possible because the signability of ring signature is not disposed and a group for ring signature cannot be created right away.

RSA algorithim is the same as a ring signature, in that the number of users in a group is one.

Let’s take a look at the composit function C_k,v (y1, y2, y3, .., yn).

Here, k means a key and v is an initial value. y1, y2, y3, ... , yn are random values.

Let’s make the result value for the composit function as z.

In brief, C_k,v (y1, y2, y3, .., yn) = z

Solving this mathematic formula for a simple entry is not difficult.

However, if y1、y2、y3、...、yn is a trapdoor function, meaning if y1 = g(x1)、y2 = g(x2) …, yn = g(xn), it is difficult to find x1、x2、x3, … , xn that satisfies the above.

This is because y1=g(x1)is a trapdoor function.

This type of function is called a ring equation and is defined as follows:

C_k,v (y1, y2, y3, .., yn) = Ek(yn • Ek(y(n-1) • Ek(…• Ek(y1 • v) …)) = v

Ring signature can be separated into roughly six phases.

Assuming P1, P2, ... , Pni is a ring’s public key;

1. A key is generated. K= Hash(m), where m means plain text.
2. A random string v is generated. 
3. A random value Xi that applies to all the members (excluding yourself) in a group is generated. Yours (Xs) will be calculated as your own PrivateKey. And, Yi=g(Xi) applicable to Xi will be calculated. 
4. Solve a ring formula that is applicable to Ys. Since Yis are known, it is easy to solve the ring formula.
5. Xs is found. Xs = g^-1(Ys)
6. The result of the ring signature is as follows: (P1, P2, … , Pn, v, X1, X2, …, Xn)

Ring verification is divided into three phases:

1. For Xi, find Yi=gi(Xi)
2. Find a key, K = Hash(m)
3. Verify to see if the ring equation is valid. C_k,v (y1, y2, y3, .., yn) = v

When a user wants to remove anynomity, it is possible for the user to prove to be a true signer by clarify his/her own seed value and x_s to a verifier. This way the verifier may be able to use the seed value to calculate x_s and know that one value does not exist in the value of x_s being sent from the user. The value is the value of x_s, and by comparing it with the x_s value of the signer, the anynomity can be removed.

In ring signature Tx, on a recipient’s behalf, a sender generates a random one-time address (One-Time Address) for all transactions.

A recipient can always generate one address only, and all the expenses received will be transferred to a particular address that is not related to the reciepient’s address.

The transfer location of the expense can only be decided by the sender by and the receiver via a stealth address.

A stealth account is composed of an individual display key, non-public expense key and address.

An expense key is used when using your own account to pay with coins. The display key displays the receipt history of the account.

Also, an address is used to generate a recipient’s address.

An address is generated by the payment key and the display key.

For example, in blockchain in which stealth address is supported, assuming User A has n units of tokens. User A may be able to use those tokens however ways he wants.

Let’s assume that A is going to send those tokens to User B. When sending those tokens, the transaction is output and inform the network on the fact that A is sending n units of tokens to User B.

Then, B becomes a legitimate owner of n units of tokens. A stealth address is dynamic, meaning it consists of a combination of various one-time public keys and secret keys. User A’s wallet uses User B’s public key as well as his secret key. Then, letters are generated to ceate a one-time public key for User B’s output. This way, other users on the network may see that such transaction is being recorded, but they may not know that n units of tokens are traded other than that fact that User A and User B are involved in this transaction.

During the transaction, User A may put tokens in his wallet by fininding the transaction details from blockchain through his own wallet’s secret key. B may use a one-time secret key to obtain a right to use those tokens. During the process, neither the sender nor the receipent’s wallet address are not disclosed anywhere.

As described in the above, a one-time address is generated instead of the receipient’s original address. By this, a stealth address can realize an additional protection function for personal information.

There are following upsides and downsides of stealth address:

- Upsides

• This is very effective to protect personal information. For a sender to represent a reciepient, a random one-time address gen be created for all transactions.
• Anonymity can be guaranteed. Through a one-time receiving address, money can be sent. Such transaction canot be traced since no connection can be established between a sender’s address and a receipient’s address.
• The possibility of connectivity between users is eliminated. When money is being sent, a receipient’s public address and key information are combined with a public key. During this process, a stealth address and a one-time key are auto generated.After a transaction is executed, such transaction information will be disclosed on blockchain, but speficific transaction details can be known only by the sender and the receipient.

- Downsides

• Malicious use of stealth address: if a person knows a user’s address who participates in an illegal-like malicious activity, it is an easy task to trace a transaction. However, if the user uses a stealth address instead, tracing would be a lot more difficult, meaning it would be much easier to engage in an illegal activity by using it.
• Equibirium actiity: This is generated when an identifying method to execute a transaction in blockchain to realize a stealth address and a user is identified. For example, let’s assume that thousands of a same donation are given to an address that is generated from a same website. It it technically difficult to find such tranactions and connect them to a specified user.

- Basic Stealth Address Protocol (BSAP)

There are two major problems in the basic stealth address protocol design. First, a temporary address needs to be fixed between two communication objects, meaning it is easy to connect a transaction between two objects. This also means both 2nd sender and a reciepient can calculate a secret key c.

As a result, if a fund collector does not accept such transaction within set hours (pending state), a sender may be refunded if he changes his mind during this time. Here is how it works.

A sender and a receipient each have private/public key pairs (a, A) and (b, B). Here, A = a × G, B = b ×G and G are reference points for an elliptic curve group.

The sender and the receipient together can calculate a shared secret c by using elliptic-curve Diffie-Hellman (ECDH). For c = H (a × b × G) = H (a × B) = H (b × A), H (×)is a cryptographic hash function.

A sender simply uses c x G for a stealth address so that he could send funds.

A receipient insepcts blockchain in real time to see if there is any transaction that is transferred to a destination address “c x G”. If there is such a transaction, the receipient may accept it by using the secret key c.

- Improved Stealth Address Protocol (ISAP)

An improved stealth address protocol is the above-mentioned basic stealth address with the protocol design defect being revised.Still, the blockchain node needs to monitor the blockchain with the address “c x G + B” created by using a secret key c.

This conflicts with a general logic to safely save a secret key; if a secret key continues deriving, the risk of damages increases drastically.

The derivative technology of an additional key is as follows:

A receipient has a private/public key in pair (b, B). Here, B = b × G and G are reference points for a elliptic curve group.

A sender generates a temporary key pair (r, R). Here, R = r × G is transferred along with a transaction.

The sender and the receipient together can calculate a shared secret c by using elliptic-curve Diffie-Hellman (ECDH). For c = H (a × b × G) = H (a × B) = H (b × A), H (×)is a cryptographic hash function.

The sender uses c × G + B for a temporarly destination address for settlement.

A receipient insepcts blockchain in real time to see if there is any transaction that is transferred to a destination address “c x G + B”. If there is such a transaction, the receipient may accept it by using the secret key “c + B. The temporary secret key “c + b” can only be calculated by the receipient.

- Dual-Key Stealth Address Protocol (DKSAP)

When fee pool (or a proxy server) exists in blockchain, in dual-key stealth adrses protocol, a recipient sends a number of shared secret keys and a public key so that a transaction in the blockchain ca be searched by the fee pool (or the proxy server) and its entity.

No one else can calculate a temporary secret key “c+b” on behalf of the receipient. One-time payment addresses for a transaction are as follows:

A receipient has two key pairs (s, S) and (b, B), in which S = s × G and B = b × G are search public key and a public key generation (a key for decrypting amount to be transferred) respectively. Here, G is a reference point for an elliptic curve group

A sender generates a temporary key pair (r, R), in which R = r × G will be transferred along with the transaction.

Both the sender and the receipient may use elliptic-curve Diffie-Hellman (ECDH) to calculate a shared secret c. c = H (r × s × G) = H (r × S) = H (s × R), and here H (×) is an encryption has function.

The sender uses “c x G + B”for a temporary destination address for settlement.

The receipient actively watches blockchain to see if a part of the transaction is transferred to the destination address “c x G + B”. Depending on a wallet’s encryption, the receipient can calculate the same subject address in 2 methods, which is c × G + B = (c + b) × G. If there are items that match, the secret key “c + b” can be used for payment.The temporary secret key “c + b” can only be calculated by the recipient.

Ring CT can be used to hide a balance during transaction.

Ring CT(Ring Confidential Transaction) is introduced for the purpose of realizing users’ request of not disclosing account/amount information for a transaction. Ring CT allows users to use a ring signature to execute encryption by using a specific key for an account that receives a sender’s address information and a transferred amount in a general transaction. The encrypted data can only be decrypted in the account.

Unlike a general transaction, ring CT generates input/output entries related to a stealth account using a ring signature and transfer such entries.

Transfers using ring CT can be roughly classified into three.

1 - Transfer coins from a general account to a stealth account

2 - Transfer coins from a stealth account to a general account

3 – Transfer coins from a stealth account to another stealth account

An encryption method differs slightly for every method.What is common is that a transferred amount information cannot be known except for a user making a transfer and a stealth user.

The process of ring CT encryption and decryption is as follows:

For the group of m units of addresses/commitments which are expressed as

{(P_π¹,C_π¹), (P_π²,C_π² ),…,(P_π^m,C_π^m)}, let’s assume that a secret key for each address is x_j,j=1…m .

Let’s assume that there are q+1 units of such groups in the above.

For the group of q+1, the result obtained by ring signature is exressed as:

The ring signature which is generated by the above process can only be verified by P_π^j,j=1,…,m, which is encrypted by ∑ calculation. The size of such ring CT transaction is smaller than a general transaction. The higher the number of m, the bigger the difference is.

In addition,the size can be increased to be its optimal size because it does not require the use of a key image such as a specific key file of that size is big for safer signature verification.

Next, let’s take a look at the encryption of an amount using ring CT.

One of the advantages for using ring CT is that a transferring amount that is dislosed in scalar quantity in a general blockchain can be encrypted so that only a sender and a collector can see it.

For example, when a value of a public key is P and the transferring volume is a, let’s think about a pair (P,xG+aH ) that is added to a transaction. When a transaction is generated, it is necessary to check if a value that multiplies a mask value H by a transferred volume a and a secret key x becomes xG+aH. The transferred volume can be checked during the first phase of the generation, but after being reflected to the transaction, the volume can no longer be checked and other users cannot see the transfer volume as a result. For such a pair, a averification such as a range verification is not necessary.

Next, let’s take a look at fees when using Ring CT.

In blockchain, a sender has to pay fees for each transaction. In case of ring CT, a mask must not be removed for fees. For example, fees shall be paid like bH, being paid without requiring masking, not promoting encryption such as xG+bH, which is a general amount encryption.

In other words, it is good for fees to be standardized at some degree, and a sender needs to check if his balance is larger than the fees and the transferred amount combined.