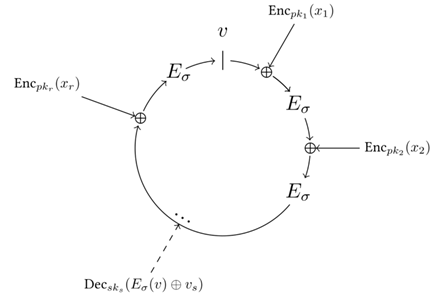
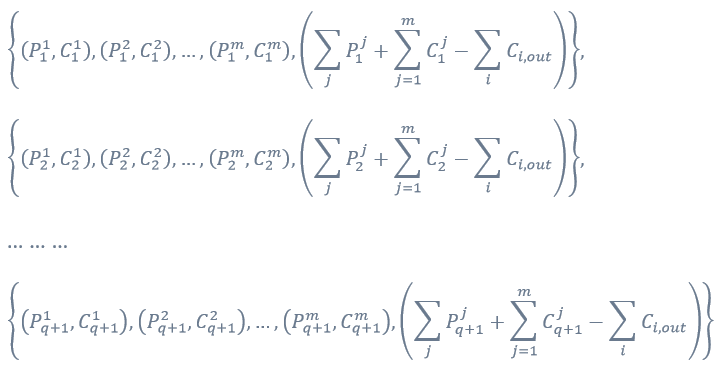QURASブロックチェーンは取引内容についての暗号化を実現して取引の匿名化を実現した。
取引の匿名化で基本問題点はConsensus Nodeから暗号化された取引内容に対する検証をどのように実現するかである。
つまりConsensus Nodeは暗号化された取引について復号化キーを利用しなくて暗号化された取引が正確だということを証明することができなければならない。
これを実現するためにZero-Knowlegde Proofというゼロ知識暗号化アルゴリズムを利用してConsensus Nodeで実の復号化キー(Private key)がなくても暗号化された取引に対する正確性を検証できるようになる。
ZK-SNARKSはこのZKPを実現したモジュールである。
まずはZero-Knowledge Proofの概念について見ることにしよう。
ゼロ知識証明方法は暗号理論で誰かが相手にどのような式が真であることを証明する際、そのいかなる情報も露出させなくて相手に真ということを認識させる方式である。
どんな式が真であることを証明しようとする側を証明者(prover)として、証明過程に参加して証明者と情報をやりとりする方を検証者(Verifier)という。
ゼロ知識証明に参加する証明者が検証者を騙すことが目的でプロトコルを変更する場合、証明者が不正直という。その他の場合には正直という。
ゼロ知識証明は次のような3つの性質を満足させなければならない。
ゼロ知識証明は確率論に依存することになる。
代表的な例としてAli Baba洞窟問題がある。
つまりProverとVerifierの間に証明施行の数が増えれば式の証明の正確度が高くなる。
しかしProverとVerifierの間に実施数が多い証明はQURASブロックチェーンで利用するのが不便である。
確率論に基づいた証明方法はInteractive Zero-Knowledge Proofとなる。
つまり施行を多く行なって真と偽の確率として式の真と偽を判別するアルゴリズムである。
このような方式はネットの負荷など様々な問題が発生することになる。
それで提案されることになったのがNon-interactive zero-knowledge proofという概念が出るようになるだった。[7] [8]
しかし証明に対する検証は計算の推定に起因することになる。
Non-interactive zero-knowledge proofはZKFの一種としてProverとVerifierの間相互にやり取りする内容がなく検証を実施する方式である。
zk-SNARK(zero-knowledge succinct non-interactive argument of knowledge)もNon-interactive zero-knowledge proofによって出た概念であり、Zcashでも利用されている。
ゼロ知識と関連した文書が多く公開されているからこれに対する具体的な内容はReferenceを参照して欲しい。
ZK-SNARK(Zero-Knowledge Succint Non-interactive Argument of Knowledge)はProverとVerifierの間にどんな情報も交換しないながらProverが証明式を作ってVerifierに検証できるモジュールを提供するが、その証明式にはProviderが実例としてSecret keyを持っているということを知らせることができるアルゴリズムである。
この時Verifierは証明式でProverのSecret Keyとかどんな情報も見いだすことができない。
ZKP(Zero Knowledge Proof)はProverがVeriferに証明式が正しいということをそのどんな情報も与えず、検証させる方式である。
実例としてランダム数Aに対するHash値Bがある時ProverはVerifierに自分がHash値Bに該当したAを知っているということをA値をVerifierに見せずに証明させることができるということだ。
ゼロ知識でProof of KnowledgeはProverがVerifierにAを持っているだけでなく、その値が正確だということをAを見せなくて確信させる方式を意味する。
Succinct ZKPでVerifierはProverのProofの長さに関係なくて短い時間(数ms秒)間に証明式が本当か嘘かを判別することができる。
もともとInteractive ZKPではProverとVerifierが何回にわたって通信を進めた後、証明を終わらせることができた。
つまりVerifierは検証のためにProverにいろいろとMessageを送り、その回答の結果による確率論に基づいて証明式の真と偽を判別することができた。
この時Proverが送っている応答メッセージあるいはVerifierが送るメッセージとしてはProverの秘密データを分かることはできないように設計される。
しかし、Non-interactive ZKPではProverとVeriferの間にただ一つのメッセージだけを通信して証明式の真と偽を判別できるようにする。
Non-interactive ZKPを実現するためにProverとVerifierの間にゼロ知識アルゴリズムを向けたPublic Parmemterを共有しなければならない。
このキーに対して生成はQURAS開発チームで進行し、QURASブロックチェーンで共通に利用されるようになる。
QURAS ブロックチェーンで利用したDAP(Decentralized Anonymous Payment System)について見る前に銀行による中央化された支払システムについて見ることにしよう。
Anonymous e-cash : Chaumによって初めて開発された。Chaumの理論に次のようである。Aliceと銀行がコインを持っていると仮定しよう。この時vに該当する価値のコインを作るためにAliceはまず銀行は分からないランダムの秘密番号SNを選択する。その後、Aliceの口座からv分減少させて銀行はSNを署名する。その次AliceがBobに自分のコインを送金しようとする時に彼は銀行からサインしたSNをBobに与えてその署名が実に銀行から署名したものということを証明させる。この時、Bobとか銀行はAliceのSN情報から身分情報を知ることができない。そして銀行で以前に発生したSNに対しては無効と認める規約によって二重支払いは許されない。
Unforgeable e-cash : Chaumの理論には一つの問題点があるが銀行の秘密キーが危うくなるとコインが偽造される可能性がある。これについて詳しく説明すると以下のようになる。
銀行は"Coin Commitment"としてMerkle Treeを維持してユーザは定期的にこのMerkle Treeのroot値であるrtを照会する。特に銀行はいかなる秘密資料を維持していない。Aliceがコインを要求する時、彼はランダムの秘密番号SNと補助文字列rを選択してcm:=CRH(SN||r)を計算して銀行に送る。ここでCRH は衝突回避の関数である。
銀行ではcmをもらえばAliceの口座から要請金額を削減してcmをMerkleTreeのleafノードに追加する。その後、Bobに支払うためにAliceはBobにSNとともにゼロ知識証明πを送る。
AliceはBobにSNが銀行のMerkle Treeのleafに保管されていることを知らせることができる。
しかしゼロ知識証明によってBobはAliceの身分情報が分からなくなる。後にBobはAliceから受け取ったSNとπを銀行に送る。
まずはZK-SNARKSの原理を知る前にQURASブロックチェーンでTransparent Transactionについて見てZK-SNARKSをある項目に利用してAnonymousを実現できるかを見よう。
代表的なTransparent TransactionはContract Transaction構造から見た。
Contract Transactionで基本入力はCoin Reference情報であり、出力とTransaction Outputの項目である。
QURASブロックチェーンでTransparent TransactionのFrom、To、Amount情報はContract TransactionのCoin ReferenceとTransaction Outputの項目によって得られる。
それではContract TransactionのCoin ReferenceとTransaction Outputの項目からどのようにFrom、To、Amountを決定できるのかについて見ることにしよう。
Contract Transaction構造で見るとCoin Referenceは以前に発生したTransactionのTransaction Outputに対する参照である。
つまりブロックチェーンのデータからCoin Referenceを推定して、簡単にCoin Referenceが示すTransaction Outputの項目を得ることができる。
Transaction Outputの項目は3つの項目つまりAssetID、Value、ScriptHashの項目を持つ。
つまりCoin Referenceが指したTransaction Outputの項目のScriptHashはFromのアドレスになる。
そしてContract TransactionのTransaction Outputの項目のScriptHashは最終残高状況を表示することになる。
すなわちこの項目によってToのアドレスと送金量を確認することができる。
Contract Transactionのすべての項目は暗号化されなくてそのままブロックチェーンに登録されるためからノードは発生したTransactionについてFrom、To、Amountが正確に計算できだったのか
を正確に検査することができるしSign値を確認してTransactionが偽造されなかったかどうかを確認することができる。
それではAnonymous Transactionで基本暗号化しなければならない部分について見当が行くのである。
Anonymous Transactionで暗号化しなければならない部分はまさにCoin Reference部分とTransaction Outputの項目である。
この部分についてゼロ知識証明アルゴリズムを利用すればノードはFrom、To、Amountについて推測できず、結局Transactionの匿名化が実現されるようになる。
それではどのようにCoin ReferenceとTransaction Outputを暗号化し、またそれが正確だということを他のノードでどんな検証できるかについて進めることにしよう。
QURASブロックチェーンでZK-SNARKS用のAddressとTransactionはTransparent Addressと異なる。
QURASブロックチェーンでZK-SNARKS用のAddress生成部分は上記で説明しているので省略する。
QURASブロックチェーンで前述したようにReferenceとOutputの部分は全て暗号化されることになる。
すなわち、検証者はこの暗号化された内容をPrivateKeyがなく検証して正確であることを確認しなければならない。
そのためにZK-SNARKSでは新しい概念が登場することになる。
それはCommitmentとNullifierである。
QURASブロックチェーンで暗号化された残高をNoteと表示しよう。この時Noteの概念はBitcoinからUTXOのような概念で見ることができる。
ただNoteはUTXOのような透明性ではなく暗号化されている。
VerifierがどのようにNoteを検証するかを見ることにしよう。
AnonymousのTransactionでCommitmentとNullifierという概念が登場する。
CommitmentはUnspent Noteと考えればいいが,BitcoinではUnspent UTXOと同じである。
Nullifierは二重払いを防ぐために出たものであるがSpent Noteである。
Transactionで入力として入ったReferenceはそれのhashをNullifierでブロックチェーンに公開する。
Transaction OutputはそれのHash値でCommitmentをブロックチェーンに公開することになる。
ハッシュ関数は一方向関数としてx->YからxによってY値を求めることはできても反対が難しい種類の関数を意味する。
ZK-SNARKSでハッシュ関数を多く利用する。
まずCommitment Merkle Treeでハッシュ関数を利用する。
JoinSplitのCommitment値をleafにしてバイナリツリーを形成してMerkle Treeを構成することになるが,この時ハッシュ関数を利用するようになる。
またJoinSplitでhSigを計算する時もハッシュ関数を利用するようになる。
PRF関数(PSEDUO RANDOM FUNCTION)PRF 関数は無作為ランドーム関数を示す。
QurasブロックチェーンではC#の無作為ランドーム関数に基づいてPRFを再構築した。
JoinSplitを生成するのにPRFをたくさん利用する。
それは暗号化されたCencに対する予測不可能とCommitmentの重複現象を防ぐためにPRFを利用することとなった。
PRF関数の特徴はx値が違えばPRF(x)の結果もいつも変わらなければならない。
AUTHENTICATED ONE-TIME SYMMETRIC ENCRYPTIONAuthenticated One Time Symmetric Encryptionを簡単にSYMで表現するようにしよう。
SYM.K(SYMのキーを意味)により平文SYM.PをSYM.Cに暗号化する時SYMは次のように定義される。
SYM.Encrypt : SYM.K × SYM.P=> SYM.C に変換させる関数である。
SYM.Decrypt : SYM.K × SYM.C=> SYM.P に変換させる関数である。
この種類のSYM関数はただ一度だけ利用することを勧める。
この関数はSYM.Kが公開されると攻撃者から攻撃を受けることができるのでただ一度だけ使用することを勧告する。
KEY AGREEMENTKey Agreement 形式は二人の間で(A,Bと仮定)Aのprivate keyとBのpublic keyを利用して互いに共有された秘密資料を約束する暗号学のプロトコルである。
つまりAとBのキーを利用してAとBだけがわかる秘密資料を互いに共有できるようにしようというのである。
すなわち三者はAとBが共有した秘密資料が分からなくなる。
Key Agreement形式(簡単にKAという)は次のような3つの要素として具現される。
次の関数を定義してKAを見るようにしよう。
Key Agreement プロトコルはDiffie–HellmanのKey Exchange思想をベースにして解決して出たものである。
Diffie–HellmanのKey Exchange プロトコルでは二人のAとB間にキーを交換するがこのときAとBに対する認証ができないという弱点がある。
すなわちKey Exchange プロトコールを利用してAとB 間の匿名キーの交換が可能であるがAとB間の他のCが仲間に入れて盗聴する場合に脆弱になる。
AとBの間の鍵交換にCが仲間に入れてAとCがキーの交換を行いし、CとBがキーの交換を行ってCはAとBの間でやり取りされるデータを盗聴できるようになる。
対策としてAとBを認証するために三者の認証機関で発給されたキーで署名して送る方式でAとB間の互相認証を行うことができる。すなわち三者Cが仲間に入れる現象を防ぐための方法である。
KEY DERIVATIONKey Derivation関数はKey AgreementとAuthenticated One-Time Semmentric Encryptionを結合して定義した関数である。
この関数はKey Agreementと複数のargumentを組み合わせて作られたshared secretデータと暗号化に利用されるキーを生成する。
KDF(Key Derivation Function)を次のように定義する。
{1… N} × Bytes(hSig) × KA.SharedSecret × KA.Public × KA.Public => Sym.K
上記の関数がKDF関数である。
それではKDFを満足させなければならないセキュリティ条件を見ることにしよう。
上記の方式に基づいてESKとEPKを生成する。
KDFを利用してコインの送信者と受信者との間で公開秘密キーを生成してその情報をTransaction に反映することとして受信者だけが暗号が解読できるようにする。
SIGNATURESig関数を次のように定義しよう。
上記のSig関数を利用して送信者はトランザクションを作ってトランザクションを署名して転送する。
ZERO-KNOWLEDGE PROVING SYSTEMゼロ知識証明システムは証明者が検証者にいかなる情報も露出させずに自分の正確性を証明させる暗号学プロトコルである。
ゼロ知識証明システムはzk-SNARKSに基づいてQURAS ブロックチェンジでTransactionを暗号化して検証するのに利用された。
Qurasブロックチェーンではzk-SNARKSを利用するために次のキーを先に生成する。
つまり検証者はZK.ProvingKeyとZK.PrimaryInput、ZK.AuxiliaryInputを利用してZK.Proofを作ってそのZK.ProofデータとZK.PrimaryKeyをTransactionに入れて転送する。
Transactionを受けて検証する側はZK.VerifyingKeyとTransactionに含まれているZK.PrimaryInput、ZK.Proofを利用して当該証明結果がTrueであるかFalse であるかによって処理できる。
ZK-SNARKS KEYは次の4つの要素を持つ。
ask, apk, skenc, pkenc
ここで askは送信キーとして32byteのランドームバイト列である。
残りの3 つのキーであるpk, skenc, pkencは全部a_skから生成されることになる。
生成原理は次の通りである。
a_pk= PRF_addr(ask,0)
skenc=KA.PrivateKey(PRFaddr(ask, 1)
pkenc=KA.PublicKey(skenc, KA.Base)
ここでPRF関数とKA関数は上記で説明したのでここで言及しない。
暗号化Transactionには1つ以上のJoinSplit項目が存在する。
もし暗号化されたTransactionの場合Transactionに1つ以上のJoinSplit項目とJoinSplitSig、JoinSplitPubKey が含まれている。
検証者はJoinSplitSigとJoinSplitPubKey、JoinSplitを通してJoinSplitの正確性を検証する。
またJoinSplitの項目からZK-SNARKS Verify Key を利用して当該JoinSplit内容に対する正確性の検証、すなわちゼロ知知の証明を進める。
それではJoinSplitにどのような項目が存在するかを見てみよう。
VAmount_OldとVAmount_Newは全部1以上の値になってはならない。
もし二つの値が全部1以上の場合、Transactionは失敗と認める。
またJoinSplitのProofとZK-SNARK Verify Keyを通じてZK-SNARKS認証を行ってTrueの場合にはTransactionを成功として判断する。
Trueではないの場合にはTransactionを失敗として判断する。
暗号化されたTransaction は少なくとも一つ以上のJoinSplit項目を含めて構成することになる。
JoinSplitを構成する段階で第一段階はJoinSplitを検証するための署名キー(JoinSplitSig)のためのキーペアを先に生成しなければならない。
キーペアであるJoinSplitPrivKeyとJoinSplitPubKeyをECCアルゴリズムに基づくキー生成として生成する。
その後JoinSplitの項目を構築する。
JoinSplitの項目には2つのInputと2つのOutputから構成される。
送信者はInput項目を次のように構成する。
Inputを生成しながらhsigを生成する。そしてランドームバイト列を生成してそれに基づいてOutPutを生成する。
Outputを生成する段階は以下の通りである。
ここでInputとOutputにランドーム文字列を入れるのは暗号解読を困難にするためのものである。
つまり当該Noteに対して残高とアドレスが同じであっても生成されたNoteの暗号化されたデータはランドーム文字列によって異なる。
これでユーザたちが同じNoteということを知らせないためにランドーム文字列を入れたのである。
JoinSplit生成を完了するとJoinSplitボディ部分をJoinSplitPrivKeyでサインをする後TransactionにJoinSplitSigを入れてTransactionの生成を完了してブロックチェーンにbroadcastするようになる。
Note Commitment treeの深さをMerkleDepthと仮定する。
Merkle treeの毎ノードはハッシュ値で構成される。
高さがhであるMerkle treeは最大Pow(2,h)個のノードを持ち、最小Pow(2,h-1)個のノードを持つ。
マックルツリーで最後の階にあるノードを"葉ノード"と呼ぶ。
マックルーツリーで葉ノードとルートノードを除いたノードをInternalノードと呼ぶ。
M(h,i)をh層のi番目ノードとしよう。
この時M(h,i)の計算公式は以下の通りである。
M(h, i) = MerkleHash(M(h+1, 2*I), M(h+1, 2*I + 1))
QurasブロックチェーンではMerkle TreeのAuth Path理論に基づいてマクルトリーのルート値とMerkle Treeの正確性を検証できる。
Anonymous transactionでJoinSplit項目があることは上記で述べた。
JoinSplit項目のVAmount_oldはTransparent balance poolでコインを抜くことを意味するし、VAmount_newはTransparent balance poolにコインを入れる動作を意味する。
ユーザは単にJoinSplitのVAmount_oldとVAmount_newを通じてQurasブロックチェーンの全体Transparent balance poolの残高だけが測定できる。
その他の該当アカウントの残高は照会できない。
JoinSplit では暗号化されたNote単位でアカウント管理を進める。
すべてのNoteはブロックチェーンに暗号化されたまま保管されており、この暗号はただ当該アカウントのキーを持っているユーザだけが照会できる。
Anonymous Transactionには1つ以上のJoinSplit項目を持っているがこのTransactionがブロックチェーンに入る時にJoinSplitのCommitmentがブロックチェーンのNote Commitment Merkle Treeに追加されることになる。
またJoinSplitのNullifierはブロックチェーンに登録されることになる。
もしAnonymous Transactionがブロックチェーンに登録する際に当該TxのNullifierが既にブロックチェーンに登録されている場合、Double spendと認めてTransactionをブロックチェーンに登録せずに失敗に戻す。
Nullifer計算において当該Noteにランダム文字列を入れることとして同じNoteに対してもNullifierの値は異なるからNullifierとしてDouble spendを防止することになる。
Ring signatureアルゴリズムはグループに参加しているキーを有しているすべてのユーザによって署名して行われる電子署名アルゴリズムの一種類である。
リング署名の方式ではキーを持つグループのユーザのうちどんなユーザによって署名できる。したがって、リング署名を利用して署名された資料は特定グループのユーザのうち誰かによって保証される。
リング署名の特徴はグループ内のどのようなユーザのキーを利用して署名されたかが分からないことである。リング署名は特にグループ署名とよく比較されるのに二つは非常に似ているが、次の特性で違いがある。
つまりリング署名されたメセッシはグループのあるユーザによって承認されることになる。リング署名の基本特性はリング署名をグループのどのユーザのキーで署名されたのか決めづらくなることである。
リング署名はグループ署名と似ているが2つの側面で差がある。
リング署名の定義は以下の通りである。
グループのすべてのユーザは共にpublic/privateキーペアをそれぞれ持たなければならない。
つまりN個のユーザのグループは(P1, S1)、(P2, S2)、•••、(Pn, Sn)で定義できる。
ではi 番目のユーザがメッセージmに対するリング署名をσとしよう。
ではすべてのユーザはリング署名σ, m, P1, P2, …, Pnに基づいてリング署名に対する検証を進めることができる。
もしリング署名が正確に計算されていたら検証で通過することになる。
グループ内のユーザたちのprivate keyが分からなければ正確なリング署名を計算することが難しい。
リング署名の構造はRing-signとRing-verifyの2つの過程で構成されている。
リング署名は署名者がグループに属しているユーザたちの公開キーだけを分かれば署名をできるので、グループメンバーを追加したり削除したりする必要がない。しかし、署名値にグループに属しているユーザたちの公開キーが含まれなければならないため、メンバーの数が増えれば、署名値もそれに比例して長くなることが短所である。
リング署名の署名性は廃棄されなくて、リング署名のためのグループはいきなり作り出すことができないため、このような応用が可能なのである。
RSAアルゴリズムはグループのユーザの数が一つであるリング署名と同じである。
それでは合成関数Ck,v (y1,y2,y3,..,yn) を見るようにしよう。
ここでkはキーであり、vは初期値である。y1、y2、y3、 ... 、ynはランダム値である。
この時この合成関数の結果値をzとしよう。
つまり Ck,v (y1,y2,y3,..,yn) = z
簡単な入力に対してこの数式を解くことは難しくない。
でももしy1、y2、y3、...、ynがtrapdoor関数の場合すなわちy1 = g(x1)、y2 = g(x2) …、yn = g(xn) の場合それをを満足するx1、x2、x3, … 、xnを求めるのは難しい。
それはy1=g(x1)がtrapdoor関数であるからである。
このような類型の関数をring方程式と呼び、次のように定義する。
Ck,v (y1,y2,y3,..,yn) = Ek(yn • Ek(y(n-1) • Ek(…• Ek(y1 • v) …)) = v
Ring署名段階を大きく6つに分離できる。
P1、P2、... 、Pnをリングの公開キーとしよう。
Ring検証段階は3つに分離される。
もし、ユーザが匿名性を取り消そうとする時は、検証者に自分のseed値と x_sを明らかにすることで、自分が本当の署名者であることを証明することができる。検証者はseed値で x_iを計算することができ、送ってきた x_i値の中に一つの値が存在しないことがわかる。その値が x_sの値であり、署名者の x_s値と比較することで、匿名性は取り消される。
リング署名Txで送信者が受信者に代わって全てのトランザクションに対してランダム一回性アドレス(One-Time Address)を生成させる。
受信者は必ず一つのアドレスのみを生成することができるし、受信されたすべての支払金は受信されたアドレスとは関係のない固有のアドレスに移動することになる。
ステルスアドレスを利用してただ送った人と受信した人のみが支払われた転送位置を決めることができる。
ステルスアカウントには個人表示キー、非公開支出キー、そしてアドレスから構成されている。
支出キーは自分のアカウントでコインを支払うのに利用されるし、表示キーはアカウントで受信された受信履歴を見られるようにする。
またアドレスは受信先のアドレスを生成するのに利用されることになる。
アドレスは支出キーと表示キーによって生成されることになる。
例えば、ステルスアドレスをサポートするブロックチェーンにおいて、Aというユーザがn 個のトークンを保有していると仮定してみよう。 この時、Aはトークンを持っているからトークンを自分の思い通りに扱うことができる。
では、AがトークンをBに送ると仮定してみよう。それでは、トランザクションを出力し、AがBにn個のトークンを送っているという事実をネットワークに知らせることになる。
Bはn 個のトークンの正当な所有者になる。ステルスアドレスは動的で,一回用に使われる多様な公開キーと秘密キーの組み合わせで作られる。AのウォレットはB の公開キーおよび秘密キーを使用する。そしてBの出力のために一回性の公開キーを作る文字が生成される。そうなれば、ネットワーク上の他のユーザは取引が記録されることを見られるが、AとBのほかにはn個のトークンが取引されるという事実を知ることができない。
この時、Aは自分のウォレットの秘密キーを通じてブロックチェーンから取引内容を見つけてトークンをウォレットに入れることができる。B は一回性の秘密キーを使用してトークンを使う権利を得ることになる。この過程のうち、どこからでも発信者または受信者のウォレットのアドレスが公開されない。
このようにして生成された一回性のアドレスが受信者の本来のアドレスに代わってできる。それによってステルスアドレスは追加の個人情報の保護機能を実現する。
ステルスアドレスには次のようなメリットとデメリットがある。
- メリット
- デメリット
- 基本ステルスアドレスのプロトコル (Basic Stealth Address Protocol, BSAP)
基本ステルスアドレスプロトコルの設計には二つの主要問題がある。第一に臨時アドレスは二つの通信オブジェクトの間で固定することになる。したがって、二つのオブジェクトの間のトランザクションを容易に連結することができる。2 番目の発信者と受信者がいずれも秘密キーcを計算できる。
結果として、集金人が制定された時間内に受付しなければ(ペンディングの状態)、発信者は心を変えて金額を返してもらうことができる。動作方法は次の通りである。
発信者と受信者はそれぞれ個人/公開キーペア(a、A)および(b、B)を有している。ここでA = a × G 及びB = b ×G 及びG は楕円曲線グループの基準点である。
発信者と受信者ともに楕円曲線ディフィーヘルマン(ECDH)を使用して共有秘密cが計算できる。 c = H (a × b × G) = H (a × B) = H (b × A)、ここでH (×) は暗号化ハッシュ関数である。
発信者は単に送金するためにステルスアドレスにc × G を使用する。
受信者はブロックチェーンをリアルタイム的に検査しながら目的地アドレス「c × G」に転送されているトランザクションがあるかどうかを確認してそんなトランザクションがある場合には、当該秘密キーc を使用して受付することができる。
- 改善されたステルスアドレスのプロトコル(Improved Stealth Address Protocol, ISAP)
改善されたステルスアドレスプロトコルは、前述の基本ステルスアドレスのプロトコルの設計欠陥を修正したものである。しかし、ブロックチェーンノードは依然として秘密キーcを使用して目的したアドレス「c × G + B」に対するブロックチェーンを監視しなければならない。
これは秘密キーを安全に保存する一般的な論理と相反し、秘密キーを持続的に派生し続けると損傷する危険が大きく増加する。
追加キーの派生技術は次の通りである。
受信者には個人/公開キーペア(b、B)があり、ここでB = b × G およびG は楕円曲線グループの基準点である。
発信者は臨時のキーペア(r、R)を生成し、ここでR = r × G はトランザクションとともに転送する。
発信者と受信者ともに楕円曲線ディフィーヘルマン(ECDH)を使って共有秘密cが計算できる。c = H (r × b × G) = H (r × B) = H (b × R)、ここでH (×) は暗号化ハッシュ関数である。
発信者は決済のために臨時の目的地のアドレスにc × G + Bを使用する。
受信者はブロックチェーンをリアルタイム的に検査しながら、どのようなトランザクションがアドレス「c × G + B」に転送されたかを確認する。転送されたことがあれば当該秘密キー「c + b」を使用して受付ができるし、臨時の秘密キー「c + b」は受信者のみ計算できる。
- 多重キーステルスアドレスのプロトコル(Dual-Key Stealth Address Protocol, DKSAP)
Fee Pool(またはプロキシサーバ)がブロックチェーンに存在する場合、多重キーステルスアドレスのプロトコルにおいて受信者は共有する秘密キーの個数と公開キーを送るFee Pool(またはプロキシサーバ)とその実体にブロックチェーンのトランザクションを検索できるようにする。
受信者に代わって臨時秘密キー「c + b」を計算して支払えない。トランザクションに該当した一回性の支払アドレスには次の通りである。
受信者は二つの個人/公開キーペア(s、S)および(b、B)を有し、ここでS = s × G およびB = b × G はそれぞれ検索公開キーおよび公開鍵支出(転送する金額復号化に対するキー)である。ここでGは楕円曲線グループの基準点である。
発信者は臨時きーペア(r、R )を生成し、ここでR = r × G はトランザクションとともに転送する。
発信者と受信者ともに楕円曲線ディフィーヘルマン(ECDH)を使って共有秘密cが計算できる。c = H (r × s × G) = H (r × S) = H (s × R)、ここでH (×) は暗号化ハッシュ関数である。
発信者は決済のために臨時目的地のアドレスに「c × G + B」を使用する。
受信者はブロックチェーンを積極的に監視し、一部のトランザクションが目的地のアドレス「c × G + B」に転送されているかを確認する。ウォレットの暗号化如何によって受信者は同一の対象アドレスを2つの方式、すなわちc × G + B = (c + b) × G で計算でき、一致する項目があれば当該秘密
キー「c + b」を使用して支払うことができる。臨時秘密キー「c + b」は受信者のみ計算できる。Ring CTを利用してTransactionで残高を隠すことができる。
Ring CT(Ring Confidential Transaction)はトランザクションにおいてアカウントの情報と金額の情報を公開しないユーザの要求を実現するために導入された。 Ring CT はRing署名方式を利用して一般的なトランザクションで送信者のアドレスの情報と転送する金額の情報を受信するアカウントの特定のキーを利用して暗号化し、暗号化されたデータはただ該当したアカウントでのみ復号化することができる。
Ring CTは一般的なトランザクションとは異なり、ステルスアカウントに関連する入力と出力をRingSignatureで生成して転送する。
Ring CT を利用した転送は大きく3つに分類することができる。
第一、一般的な口座からステルス口座へのコインの転送
第二、ステルス口座から一般的な口座へのコインの転送
第三、ステルス口座からステルス口座へのコインの転送
毎方式ごとに金額の情報に対する暗号化方式が少しずつ異なる。共通点は転送された金額についての情報は転送したユーザとステルスユーザ以外には誰も知らないことである。
Ring CTの暗号化及び復号化の工程は以下の通りである。
{(Pπ1,Cπ1), (Pπ2,Cπ2 ),…,(Pπm,Cπm)}というm個のアドレス/commitmentらの集まりについて、個々のアドレスに対応する秘密キーを xj,j=1…m と仮定する。
上のような集まりをq+1個あると仮定する。
この時q+1個の集まりについてRing署名を取って得られる結果を
という。
こうして生成されたRingSignatureらは∑演算によって暗号化されたものとして該当したP_π^j,j=1,…,mによってのみ認証が可能である。このようなRingCTトランザクションの大きさは一般的なトランザクションの大きさより小さく、mの個数が多いほどその差は確実になる。
それだけでなく、より安全な署名認証のために容量の大きい特定のキーファイルのようなkey-imageを利用する必要がないものとして追加サイズが最適化できると考えられる。
次にRing CTで金額の暗号化について見ることとする。
一般的なブロックチェーンでスカラ量で公開される転送金額を暗号化して送金者と集金者のみ見られるということがRingCTの重要な優点の一つである。
例えば、公開キーの値がPであり、転送量がaである時にトランザクションに追加される (P,xG+aH ) というあるペアを考える。トランザクションを生成する際、Hというmask値に転送量aを掛けて秘密キーxを掛けた値がxG+aHであるかを確認しなければならないので、生成第一段階では転送量を確認することができるが、トランザクションに反映された以降はその量を確認することができなくて、結果として転送量は他のユーザは見ることができない。このようなペアについては範囲検証のような検証を進める必要がない。
次にRingCTでの手数料について見ることとする。
ブロックチェーンで送信者は毎トランザクションに対して手数料を支払わなければならない。Ring CTの場合、手数料もやはりマスクを取ってはならない。 例えば、一般的な金額の暗号化のように xG+bH 와のような暗号化を進めるのではなく、bHのようにマスクしなくて支払われるべきである。
つまり、手数料はある程度標準化(固定された値)されることが良いし、送信者は自分の残高が手数料値に転送量を加えた値より大きいことを確認しなければならない。